Portfoliotheorie: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „'''Kurzinfo!''' Die '''Portfoliotheorie''' besagt, dass durch Mischung risikobehafteter Wertpapiere (Diversifikation) und durch Investition in so genannte ef…“) |
(→Effizienzlinie) |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Kurzinfo!''' | '''Kurzinfo!''' | ||
| + | <!-- * ''Weiterleitung'': | ||
| + | ''Hauptartikel-> [[]]'' | ||
| + | * Synonyme: ''[[]]'' --> | ||
| + | <small> </small> <u> </u> <!-- --> | ||
| − | Die '''Portfoliotheorie''' besagt, dass durch Mischung risikobehafteter Wertpapiere (Diversifikation) und durch Investition in so genannte effiziente [[Portfolio]]s eine Risikoreduktion im Vergleich zur Investition in einzelne Wertpapiere erreichen lässt. *)<!--Quelle ? --> | + | Die '''Portfoliotheorie''' besagt, dass durch Mischung risikobehafteter Wertpapiere ([[Risikodiversifikation |Diversifikation]]) und durch [[Investition]] in so genannte effiziente [[Portfolio]]s eine Risikoreduktion im Vergleich zur Investition in einzelne Wertpapiere erreichen lässt. *)<!--Quelle ? --> |
Die Portfoliotheorie ist ein [[Einperiodenmodell|Einperioden]]-[[Totalmodell|Simultanmodell]].<ref>Vgl. Aschauer / Purtscher (2010), S. 140.</ref> | Die Portfoliotheorie ist ein [[Einperiodenmodell|Einperioden]]-[[Totalmodell|Simultanmodell]].<ref>Vgl. Aschauer / Purtscher (2010), S. 140.</ref> | ||
| Zeile 7: | Zeile 11: | ||
Die [[Risiko|Risiken]] im [[Portfolio]] sind nicht additiv, sondern heben sich im Risikoverbund des Portfolios auf.<ref>Vgl. Aschauer / Purtscher (2010), S. 141.</ref> | Die [[Risiko|Risiken]] im [[Portfolio]] sind nicht additiv, sondern heben sich im Risikoverbund des Portfolios auf.<ref>Vgl. Aschauer / Purtscher (2010), S. 141.</ref> | ||
| − | Klassifiziert man Aktien nach ihrer erwarteten [[Rendite]] und der [https://de.wikipedia.org/wiki/Volatilit%C3%A4t Volatilität] ihrer Rendite, kann man für einen [[ | + | Klassifiziert man Aktien nach ihrer erwarteten [[Rendite]] und der [https://de.wikipedia.org/wiki/Volatilit%C3%A4t Volatilität] ihrer Rendite, kann man für einen [[Risikoaversion|risikoaversen]] [[Investor]] feststellen: <ref>Vgl. WPH-Edition (2018) Tz. A 349.</ref> |
* Von zwei Aktien mit derselben erwarteten Rendite wird er die Aktie mit dem niedrigeren Risiko kaufen; | * Von zwei Aktien mit derselben erwarteten Rendite wird er die Aktie mit dem niedrigeren Risiko kaufen; | ||
* von zwei Aktien mit demselben Risiko wird er die Aktie mit der höheren erwarteten Rendite kaufen. | * von zwei Aktien mit demselben Risiko wird er die Aktie mit der höheren erwarteten Rendite kaufen. | ||
| Zeile 14: | Zeile 18: | ||
Die Portfoliotheorie ist ein Teilgebiet der [[Kapitalmarkttheorie]]. Spätere Entwicklungen wie das [https://de.wikipedia.org/wiki/Single-Index-Modell Single-Index-Modell], das [[Capital Asset Pricing Model]] (CAPM) und die [[Arbitragepreistheorie]] sind Weiterentwicklungen der Portfolio-Selection-Theorie.<ref>[https://de.wikipedia.org/wiki/Portfoliotheorie Wikipedia, Stichwort: Portfoliotheorie], abgefragt 10.1.2022.</ref> | Die Portfoliotheorie ist ein Teilgebiet der [[Kapitalmarkttheorie]]. Spätere Entwicklungen wie das [https://de.wikipedia.org/wiki/Single-Index-Modell Single-Index-Modell], das [[Capital Asset Pricing Model]] (CAPM) und die [[Arbitragepreistheorie]] sind Weiterentwicklungen der Portfolio-Selection-Theorie.<ref>[https://de.wikipedia.org/wiki/Portfoliotheorie Wikipedia, Stichwort: Portfoliotheorie], abgefragt 10.1.2022.</ref> | ||
| + | |||
| + | ''siehe auch-> [[Risikodiversifikation]]'' | ||
== Bedeutung == | == Bedeutung == | ||
| Zeile 31: | Zeile 37: | ||
<small> </small> <u> </u> <!-- --> | <small> </small> <u> </u> <!-- --> | ||
| − | Die '''Effizienzlinie''' ist der geometrische Ort aller effizienten Ertrags-Risiko-Kombinationen.<ref>[https://de.wikipedia.org/wiki/Portfoliotheorie#Effiziente_Portfolios Wikipedia, Stichwort: Portfoliotheorie], abgefragt 8.2.2022.</ref> | + | Die '''Effizienzlinie''' ist der geometrische Ort aller effizienten Ertrags-Risiko-Kombinationen.<ref>[https://de.wikipedia.org/wiki/Portfoliotheorie#Effiziente_Portfolios Wikipedia, Stichwort: Portfoliotheorie], abgefragt 8.2.2022.</ref> Sie stellen [https://de.wikipedia.org/wiki/Pareto-Optimum Pareto-Optima] dar. |
Ein [[Portfolio]] heißt effizient, wenn kein anderes Portfolio existiert, welches bei gleicher [[Rendite]]erwartung ein geringeres [[Risiko]] bzw. bei gleichem Risiko eine höhere Rendite hat.<ref>[https://de.wikipedia.org/wiki/Portfoliotheorie#Effiziente_Portfolios Wikipedia, Stichwort: Portfoliotheorie], abgefragt 8.2.2022.</ref> | Ein [[Portfolio]] heißt effizient, wenn kein anderes Portfolio existiert, welches bei gleicher [[Rendite]]erwartung ein geringeres [[Risiko]] bzw. bei gleichem Risiko eine höhere Rendite hat.<ref>[https://de.wikipedia.org/wiki/Portfoliotheorie#Effiziente_Portfolios Wikipedia, Stichwort: Portfoliotheorie], abgefragt 8.2.2022.</ref> | ||
| Zeile 37: | Zeile 43: | ||
[[Risikoavers]]e Investoren werden ihr Vermögen - entsprechend ihrer individuellen Risikoeinstellung - ausschließlich in Portfolios investieren, die auf der Effizienzlinie liegen.<ref>Vgl. WPH-Edition (2018) Rz A 349.</ref> | [[Risikoavers]]e Investoren werden ihr Vermögen - entsprechend ihrer individuellen Risikoeinstellung - ausschließlich in Portfolios investieren, die auf der Effizienzlinie liegen.<ref>Vgl. WPH-Edition (2018) Rz A 349.</ref> | ||
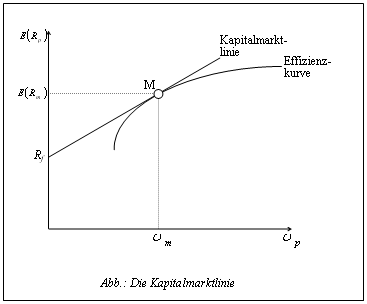
| − | [[Datei:Cml.png| | + | [[Datei:Cml.png||Das Marktportfolio M]] |
== Literatur == | == Literatur == | ||
Aktuelle Version vom 10. November 2024, 08:30 Uhr
Kurzinfo!
Die Portfoliotheorie besagt, dass durch Mischung risikobehafteter Wertpapiere (Diversifikation) und durch Investition in so genannte effiziente Portfolios eine Risikoreduktion im Vergleich zur Investition in einzelne Wertpapiere erreichen lässt. *)
Die Portfoliotheorie ist ein Einperioden-Simultanmodell.[1]
Die Risiken im Portfolio sind nicht additiv, sondern heben sich im Risikoverbund des Portfolios auf.[2]
Klassifiziert man Aktien nach ihrer erwarteten Rendite und der Volatilität ihrer Rendite, kann man für einen risikoaversen Investor feststellen: [3]
- Von zwei Aktien mit derselben erwarteten Rendite wird er die Aktie mit dem niedrigeren Risiko kaufen;
- von zwei Aktien mit demselben Risiko wird er die Aktie mit der höheren erwarteten Rendite kaufen.
Die Portfoliotheorie geht auf Harry Markowitz (1952) zurück, der 1990 dafür den den Alfred-Nobel-Gedächtnispreis für Wirtschaftswissenschaften[4] erhielt.[5]
Die Portfoliotheorie ist ein Teilgebiet der Kapitalmarkttheorie. Spätere Entwicklungen wie das Single-Index-Modell, das Capital Asset Pricing Model (CAPM) und die Arbitragepreistheorie sind Weiterentwicklungen der Portfolio-Selection-Theorie.[6]
siehe auch-> Risikodiversifikation
Inhaltsverzeichnis
Bedeutung
Die Portfoliotheorie hat in der Unternehmensbewertung keine praktische Bedeutung mehr.
Effizienzlinie
siehe auch-> Kapitalmarktlinie
Die Effizienzlinie ist der geometrische Ort aller effizienten Ertrags-Risiko-Kombinationen.[7] Sie stellen Pareto-Optima dar.
Ein Portfolio heißt effizient, wenn kein anderes Portfolio existiert, welches bei gleicher Renditeerwartung ein geringeres Risiko bzw. bei gleichem Risiko eine höhere Rendite hat.[8]
Risikoaverse Investoren werden ihr Vermögen - entsprechend ihrer individuellen Risikoeinstellung - ausschließlich in Portfolios investieren, die auf der Effizienzlinie liegen.[9]
Literatur
Fachliteratur
- WPH-Edition (2018), Rz. A 349.
siehe auch -> Liste der verwendeten Literatur
Weblinks
- Portfoliotheorie bei Wikipedia, abgefragt 10.1.2022;
Einzelnachweise
- ↑ Vgl. Aschauer / Purtscher (2010), S. 140.
- ↑ Vgl. Aschauer / Purtscher (2010), S. 141.
- ↑ Vgl. WPH-Edition (2018) Tz. A 349.
- ↑ Gemeinsam mit William F. Sharpe (CAPM) und Merton H. Miller (Irrelevanzthese).
- ↑ Wikipedia, Stichwort: Portfoliotheorie, abgefragt 10.1.2022.
- ↑ Wikipedia, Stichwort: Portfoliotheorie, abgefragt 10.1.2022.
- ↑ Wikipedia, Stichwort: Portfoliotheorie, abgefragt 8.2.2022.
- ↑ Wikipedia, Stichwort: Portfoliotheorie, abgefragt 8.2.2022.
- ↑ Vgl. WPH-Edition (2018) Rz A 349.